The division of the octave in Music Theory
The distance from one to the other of these tones has been divided into twelve equal parts.
Knowing as we now do the division of the entire tone series, it being divided into nine equal sections or octaves and further more knowing as we now do the division of each of these octaves, they being subdivided into twelve equal parts, it follows that we have in all 9 x1 2 or 108 tones, and adding to this the highest tone where with to close the scale, we have in all 109 tones in practical us .
None of our instruments produce this entire range of tones, except it be the organ, and it only produce them through the aid of different stops.
Octave divisions in music theory
It has been said that the distance of an octave has been divided into twelve equal parts. It might have been divided in a larger or smaller number of tones, but the division of twelve tones was deemed best, hence it was adopted. Some nations as for instance the Arabians have smaller divisions, while others have larger ones. The distance from one of these twelve ones to the next upward or downward is called a half step or halftone.
Two of these half steps or half tones constitute a whole step or a whole tone.
As each of these twelve tones are represented on the piano by separate keys, the rule may here be laid down, in order to facilitate matters for students, that from any one key on the piano to the next following upwards or downwards is a half-step, or half-tone. This last term is rather ambiguous, as many terms adopted in musical theory are, but as it is often used, we give it here. We prefer however to us the term of half step and whole-step.
Naming music tones
Having made all the necessary divisions in the chain of 109 tones, we will proceed to name them. Were we to give each tone a separate name, it would be difficult to remember them. In order to facilitate and to simplify the study of music, the same name has been given to the first tone of each of the nine octaves. In order to make the lesson plain, we will represent the twelve divisions in the following manner:
![]()
Separate names might have been given to each of these twelve tones, but it was thought sufficient to supply only seven with them, namely the first, 3th, 5th, 6th, 8th, 10th, and 12th tones.
The 13th is merely a repetition of the 1st and as such receives the same name. If we represent the interval which have separate names in the above manner, we will have the following schedule:
![]()
We have used letters from the alphabet to name the several tones. They might have been given any other names, but it was the most natural to use the letters. In some European countries the names used, are ut, re, mi, fa, so, la, si, while in Germany the tone represented by the letter, is called h. The explanation of the cause of this would occupy too much space, and we must therefore pass on with our lessons.
Let us now represent in the same manner the tones that nave not received separate names,
![]()
Keyboard tones
Placing the two schedules above each other, we have another representation the keyboard.
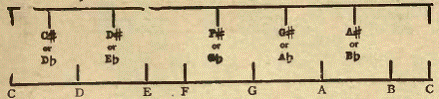
He upper lines represent the black keys, the lower the white keys. It will be observed that the upper keys have derived their names from the lower by adding sharps or flats, and that each of the upper has two names.
For this reason the names of the lower keys are called principle names, while those of the upper keys are called derived or intermediate names.
In using sharps and flats it may however so happen that the white keys also have derived names. Thus, for instance, by placing sharps below E and B, the white keys of F and C, are no longer called such, but are recognized as E sharp and B sharp. In the same manner by placing flats before C and F, the two white keys of E and B are no longer called such, but are recognized as C flat and F flat.



