Music intervals
The distance between two pitches is the interval between them. The name of an interval depends both on how the notes are written and the actual distance between the notes as measured in half steps.
The distance between pitches
The interval between two notes is the distance between the two pitches – in other words, how much higher or lower one note is than the other. This concept is so important that it is almost impossible to talk about scales, chords, harmonic progression, cadence, or dissonance without referring to intervals. So if you want to learn music theory, it would be a good idea to spend some time getting comfortable with the concepts below and practicing identifying intervals. Scientists usually describe the distance between two pitches in terms of the difference between their frequencies. Musicians find it more useful to talk about interval. Intervals can be described using half steps and whole steps. For example, you can say “B natural is a half step below C natural”, or “E flat is a step and a half above C natural”. But when we talk about larger intervals in the major/minor system, there is a more convenient and descriptive way to name them.
Naming music intervals
The first step in naming the interval is to find the distance between the notes as they are written on the staff. Count every line and every space in between the notes, as well as the lines or spaces that the notes are on. This gives you the number for the interval. Figure 1

To find the interval, count the lines or spaces that the two notes are on as well as all the lines or spaces in between. The interval between B and D is a third. The interval between A and F is a sixth. Note that, at this stage, key signature, clef, and accidentals do not matter at all. The simple intervals are one octave or smaller.
Simple Intervals

If you like you can listen to each interval as written above: prime, second, third, fourth, fifth, sixth, seventh, octave. Compound intervals are larger than an octave.
Compound Intervals
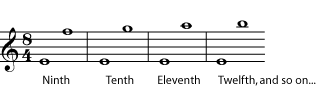
Listen to the compound intervals shown: ninth, tenth, eleventh. Figure 5

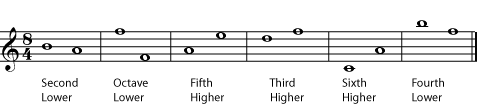
Classifying intervals
So far, the actual distance, in half-steps, between the two notes has not mattered. But a third made up of three half-steps sounds different from a third made up of four half-steps. And a fifth made up of seven half-steps sounds very different from one of only six half-steps. So in the second step of identifying an interval, clef, key signature, and accidentals become important. Figure 8:

A to C natural and A to C sharp are both thirds, but A to C sharp is a larger interval, with a different sound. The difference between the intervals A to E natural and A to E flat is even more noticeable.
Listen to the differences in the thirds and the fifths that are written above. So the second step to naming an interval is to classify it based on the number of half steps in the interval. Familiarity with the chromatic scale is necessary to do this accurately.
Perfect Intervals
Primes, octaves, fourths, and fifths can be perfect intervals. Note: These intervals are never classified as major or minor, although they can be augmented or diminished (see below). What makes these particular intervals perfect? The physics of sound waves (acoustics) shows us that the notes of a perfect interval are very closely related to each other. (For more information on this, see Frequency, Wavelength, and Pitch and Harmonic Series.) Because they are so closely related, they sound particularly good together, a fact that has been noticed since at least the times of classical Greece, and probably even longer. (Both the octave and the perfect fifth have prominent positions in most of the world’s musical traditions.) Because they sound so closely related to each other, they have been given the name “perfect” intervals. Note: Actually, modern equal temperament tuning throws these intervals slightly off of the pure perfect intervals, but for the purpose of identifying intervals, this does not matter. If you want to learn more, see Tuning Systems. A perfect prime is also called a unison. It is two notes that are the same pitch – the same note. A perfect octave is the “same” note an octave – 12 half-steps – higher or lower. A perfect 5th is 7 half-steps. A perfect fourth is 5 half-steps.
Perfect Intervals

Listen to the unison, octave, perfect fourth, and perfect fifth.
Major and Minor Intervals
Seconds, thirds, sixths, and sevenths can be major intervals or minor intervals. The minor interval is always a half-step smaller than the major interval.
Major and Minor Intervals
1 half-step = minor second (m2) 2 half-steps = major second (M2) 3 half-steps = minor third (m3) 4 half-steps = major third (M3) 8 half-steps = minor sixth (m6) 9 half-steps = major sixth (M6) 10 half-steps = minor seventh (m7) 11 half-steps = major seventh (M7) Example 3 Major and Minor Intervals Figure 10

Listen to the minor second, major second, minor third, major third, minor sixth, major sixth, minor seventh, and major seventh.

Augmented and Diminished Intervals
If an interval is a half-step larger than a perfect or a major interval, it is called augmented. An interval that is a half-step smaller than a perfect or a minor interval is called diminished. A double sharp or double flat is sometimes needed to write an augmented or diminished interval correctly. Always remember, though, that it is the actual distance in half steps between the notes that determines the type of interval, not whether the notes are written as natural, sharp, or double-sharp. Example 4 Some Diminished and Augmented Intervals Figure 15

Listen to the augmented prime, diminished second, augmented third, diminished sixth, augmented seventh, diminished octave, augmented fourth, and diminished fifth.

A diminished fifth and an augmented fourth are both six half-steps, or three whole tones, so another term for this interval is a tritone. This unique interval, which cannot be spelled as a major, minor, or perfect interval, is considered unusually dissonant and unstable (tending to want to resolve to another interval) in Western Music. You have probably noticed by now that the tritone is not the only interval that can be “spelled” in more than one way. In fact, because of enharmonic spellings, the interval for any two pitches can be written in different ways.
A major third could be written as a diminished fourth, for example, or a minor second as an augmented prime. Always classify the interval as it is written; the composer had a reason for writing it that way. That reason sometimes has to do with subtle differences in the way different written notes will be interpreted by performers, but it is mostly a matter of placing the notes correctly in the context of the key, the chord, and the evolving harmony. (Please see Beginning Harmonic Analysis for more on that subject.)
Figure 18

Inverting music intervals
To invert any interval, simply imagine that one of the notes has moved one octave, so that the higher note has become the lower and vice-versa. Because inverting an interval only involves moving one note by an octave (it is still essentially the “same” note in the tonal system), intervals that are inversions of each other have a very close relationship in the tonal system.
Inverting Intervals
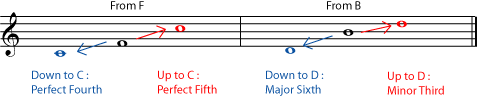
To find the inversion of an interval To name the new interval, subtract the name of the old interval from 9. The inversion of a perfect interval is still perfect. The inversion of a major interval is minor, and of a minor interval is major. The inversion of an augmented interval is diminished and of a diminished interval is augmented.
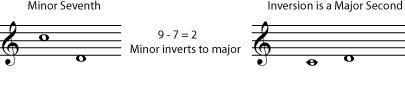
![]() Part of this page is taken by cnx.org and licensed by Catherine Schmidt-Jones under a Creative Commons License.
Part of this page is taken by cnx.org and licensed by Catherine Schmidt-Jones under a Creative Commons License.



